Abb. 1: Die Ausgangsmatrix wird mit allen Masken kombiniert
Beim Masking wird eine XOR-Maske über alle Datenmodule gelegt, die bestimmte Muster, wie das Finder Pattern, in Datenmodulen unterdrücken soll. Dadurch wird eine schnelle Erkennung des Symbols garantiert.
Eine Maske ist eine Funktion mit zwei Parametern f(x,y), die einzelne Koordinaten von Datenmodulen erwartet. Ihr Rückgabewert ist ein Boolean. Nacheinander werden die Koordinaten aller Datenmodule abgefragt, bei True wird die Farbe des Moduls umgekehrt (hell wird zu dunkel und umgekehrt), bei False passiert nichts.
Da nur die Datenmodule davon betroffen sind, werden Metainformationen, Finder-, Alignment- und Timing Patterns nicht maskiert.
Im Standard sind acht solche Funktionen für die XOR-Maske vorgesehen und alle sind in Tabelle 1 dargestellt. Zusätzlich zum eigentlichen Maskierungsvorgang wird die Mask Pattern Referenz in den Formatinformationen abgelegt, sodass eindeutig feststeht welche Funktion für ein Symbol gewählt wurde.
| Mask Pattern Referenz | Bedingung |
|---|---|
| 000 | (i + j) mod 2 = 0 |
| 001 | i mod 2 = 0 |
| 010 | j mod 3 = 0 |
| 011 | (i + j) mod 3 = 0 |
| 100 | ((i div 2) + (j div 3)) mod 2 = 0 |
| 101 | (i j) mod 2 + (i j) mod 3 = 0 |
| 110 | ((i j) mod 2 + (i j) mod 3 = 0 |
| 111 | ((i j) mod 3 + (i + j) mod 2) mod 2 = 0 |
Tab. 1: Mask Pattern Referenzen zu Masking Funktionen (vgl. [ISO] S. 50)
Prinzipiell ist es egal welche der Funktionen beim Masking verwendet wird, solange die Referenz richtig ist. Trotzdem sind im Standard bestimmte Kriterien hinterlegt, die helfen sollen die optimale Funktion herauszusuchen.
Abb. 1: Die Ausgangsmatrix wird mit allen Masken kombiniert
Bei der Auswahl der Maske wird zunächst eine Ausgangsmatrix mit den zu maskierenden Datenmodulen erzeugt (siehe Abbildung 1). Diese wird dann nacheinander mit allen acht Funktionen maskiert und jede maskierte Matrix wird anschließend bewertet. Die Bewertung erfolgt auf Grundlage der Tabelle 2. Wenn ein Bewertungskriterium zutrifft, werden die dazugehörigen Strafpunkte für die jeweilige Matrix hinzugezählt.
Es wird die Referenz der Maske / Funktion ausgewählt, die die wenigsten Strafpunkte hat.
| Eigenschaft | Bewertungskriterium | Punkte |
|---|---|---|
| Hintereinander liegende Module in Zeile / Spalte haben die gleiche Farbe | Anzahl der gleichfarbigen Module = (5 + i) | 3 + i |
| Block mit Modulen in gleicher Farbe | Blockgröße = m * n | 3 * (m - 1) * (n - 1) |
| 1:1:3:1:1 Muster in Zeile / Spalte | 40 | |
| Verhältnis helle zu dunkle Module im gesamten Symbol | 50 (5*k)% zu 50±(5*(k+1))% | 10 * k |
Tab. 2: Bewertungskriterien mit Strafpunkten (vgl. [ISO] S. 52)
Für die Fehlerkorrektur in QR Codes wird immer ein Reed-Solomon Code (RS Code) mit Erzeugerpolynom verwendet. Dafür sind insgesamt 4 Fehlerkorrektur Niveaus vorgesehen, die zu jeder Version existieren. Sie können stets über den Indicator referenziert werden (siehe Tabelle 3). Zu einer Version muss das Fehlerkorrektur Niveau ausgewählt werden. L hat die geringste Fehlerkorrekturrate, aber es passen auch die meisten Informationen in das Symbol.
| Fehlerkorrektur Niveau | Wiederherstellungs Kapazität % |
|---|---|
| L | 7 |
| M | 15 |
| Q | 25 |
| H | 30 |
Tab. 3: Fehlerkorrektur Niveau
RS Codes werden auch in anderen bekannten Standards, wie CD (Compact Disk) oder DVB (Digital Video Broadcasting) eingesetzt. Das liegt an ihren vielfältigen Einsatzmöglichkeiten und der variablen Fehlerkorrekturrate.
Bei RS Codes wird mit Koeffizienten von Polynomen über Galois Felder gerechnet. Das bedeutet, dass zunächst ein Symbolalphabet über ein Galois Feld definiert werden muss. Im Falle der QR Codes wird immer ein Galoisfeld der Größe 2^8 (bzw. 256) verwendet. So entspricht jedes Codewort einem Element dieses Alphabets. Ein solches Element wird häufig auch Symbol genannt, sodass von Daten- und Fehlerkorrektursymbolen gesprochen wird. Diese dürfen jedoch nicht mit den QR Code Symbolen verwechselt werden.
Die notwendigen Erzeugerpolynome sind im Standard definiert und können direkt übernommen werden. Mit dem Erzeugerpolynom wird die Nachricht encodiert und um die Fehlerkorrektursymbole erweitert. Das bedeutet die Nachricht steht in Klartext da, aber zusätzlich gibt es weitere redundante Fehlerkorrekturinformationen. Diese können bei Bedarf herangezogen werden.
Beim decodieren werden die Nachricht und die Fehlerkorrektursymbole ausgelesen. Mit Hilfe mehrerer verschiedener Gleichungssysteme können zunächst die Positionen der Fehler bestimmt und diese dann anschließend verbessert werden.
Die Fehlerkorrekturrate kann bei RS Codes einfach festgelegt werden. Als Faustregel gilt, dass 2t Fehlerkorrektursymbole garantiert t Fehler korrigieren können. Dabei ist die Verteilung der Fehler irrelevant. Sogenannte Burstfehler, also längere Fehlerfolgen, können auch erkannt und behoben werden. Das ist wichtig, denn ein Fleck (z.B. Dreck oder Kaffee) auf einem QR Code verfälscht viele hintereinanderliegende Codewörter.
Es ist jedoch nicht möglich eine 100%ige Fehlerkorrekturrate zu erlangen, da auch die Korrektursymbole ebenfalls Fehler enthalten können.
Für des Generieren und Auslesen von QR Codes ist es nicht wichtig RS Codes im Detail zu verstehen, hier können auch existierende Bibliotheken genutzt werden. Es ist wichtig zu verstehen, dass RS Codes Möglichkeiten bieten Daten robust abzulegen, sodass diese auch bei Fehlern noch korrekt ausgelesen werden können. Trotzdem soll ein kleines Beispiel zumindest das Erzeugen der Fehlerkorrekturdaten bei Reed-Solomon Codes verdeutlichen.
Für das Beispiel erzeugen wir ein Galoisfeld der Größe 8 mit dem
Primitivpolynom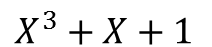 
Die
einzelnen Elemente sind in Tabelle 3 dargestellt.
Tab. 3: GF(8) des Erzeugerpolynoms (vgl. [ECC] S. 156)
Nachdem das GF(8) bekannt ist, kann im Folgenden damit gerechnet werden. Es muss bestimmt werden wie hoch die Anzahl der zu korrigierenden Fehler (bzw. die Fehlerkorrekturrate bezogen auf die Nachricht) sein soll. 2t Fehlerkorrektursymbole können t Fehler verbessern. In dem Beispiel werden 4 Fehlerkorrektursymbole berechnet, deswegen können auch garantiert mindestens 2 Fehler korrigiert werden.
Dafür wird ein Polynom benötigt, welches aus 4 Einheitswurzeln
des Galoisfeldes besteht. In dem Beispiel berechnen wir das
Erzeugerpolynom g(X) mit den vier Einheitswurzeln
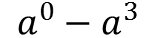. Nach ausmultiplizieren bekommen wir
das Erzeugerpolynom g(X) aus Formel 1.
For. 1: Berechnung für Erzeugerpolynom
Wie schon erwähnt werden jedoch nur die Koeffizienten der
Polynome betrachtet. In Koeffizientendarstellung ist g =
.
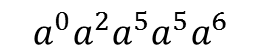In dem Beispiel möchten wir die Datensequenz 111001111
encodieren (vgl. [ECC]
S. 157). Diese Daten entsprechen dem Polynom 
in Koeffizientendarstellung.
Beim encodieren wird das Datenpolynom um so viele 0en erweitert, wie es Korrektursymbole gibt. Das erweiterte Datenpolynom wird anschließend durch das Erzeugerpolynom dividiert. Wir verwenden 4 Fehlerkorrektursymbole, also rechnen wir wie in Formel 2.
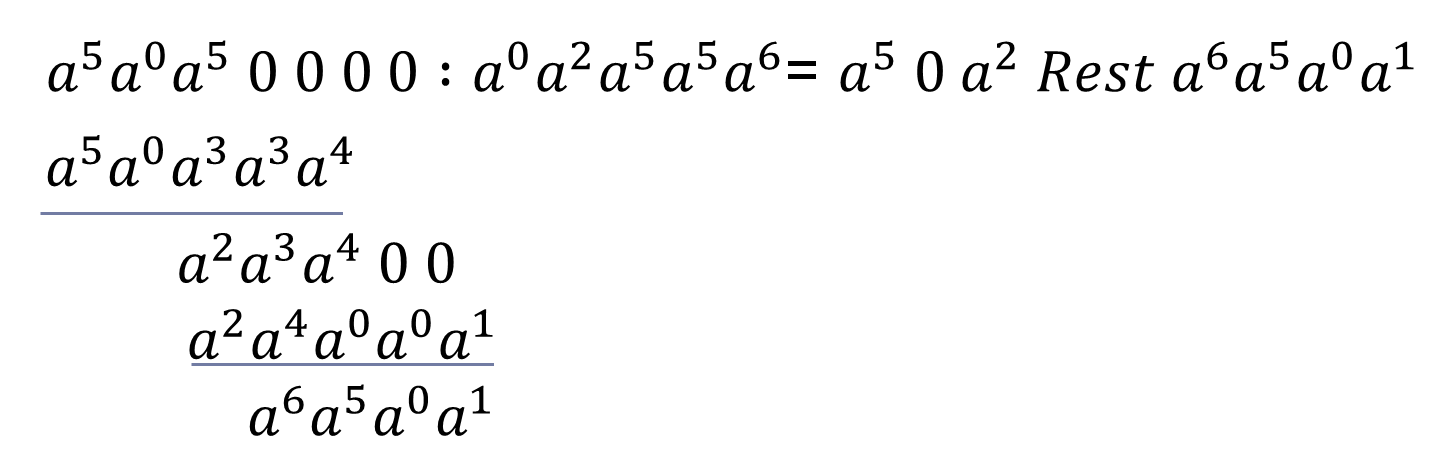
For. 2: Polynomdivision zur Berechnung der Korrektursymbole
Der Rest enthält die Fehlerkorrektursymbole. Das Ergebnis des Encodings setz sich zusammen aus dem Datenpolynom konkateniert mit dem Rest in Koeffizientendarstellung.
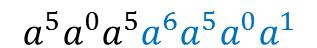=111001111101111001010
Das Decodieren ist wesentlich komplizierter als das Encodieren, da nun die erwähnten Gleichungssysteme ins Spiel kommen. Das Vorgehen wird aufgrund der vielen unübersichtlichen Rechnungen von Polynomen über Galoisfeldern nur skizziert.
Wir erhalten die Nachricht R (siehe Formel 3) mit
Fehlerkorrektursymbolen. R ist optimaler Weise ,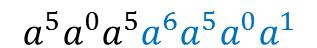
aber die Symbole könnten auch falsch sein.
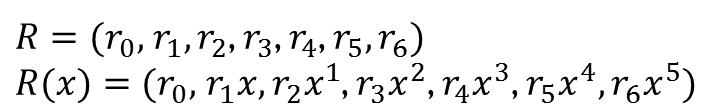
For. 3: Empfangene Daten
Dann berechnen wir die Syndrome indem wir für R(x) nacheinander die Elemente das Galoisfeldes einsetzen. Das wiederholen wir solange bis die Anzahl der Polynome den Fehlerkorrektursymbolen entspricht, so wie in Formel 4.
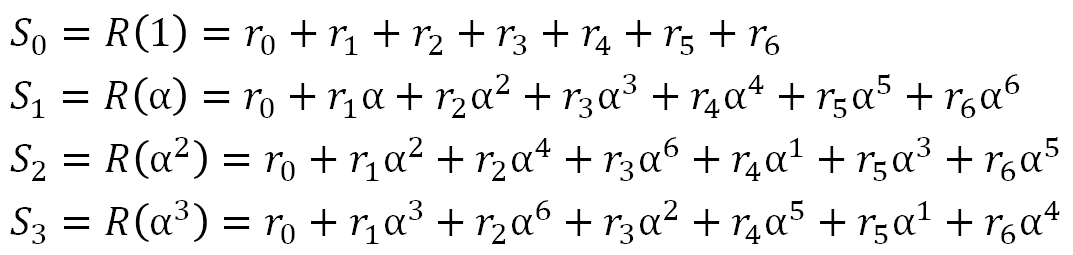
For. 4: Syndrome für das Beispiel
Dann stellen wir das Gleichungssystem zur Ermittlung der Fehlerpositionen auf. Da in unserem Beispiel bis zu 2 Fehlerkorrekturen möglich sind, muss das Gleichungssystem aus 2 Gleichungen bestehen.
For. 5: Gleichungssystem zur Ermittlung der Fehlerpositionen
Mit der Berechnung von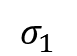 
und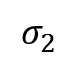 
können wir eine Funktion 
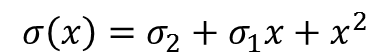aufstellen, die uns die Positionen der Fehler liefert, denn für
jeden Fehler gilt der Sachverhalt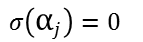 
.
Die Fehlerpositionen werden für ein weiteres Gleichungssystem
(siehe Formel 6) verwendet, in dem die jeweiligen Fehlergrößen
und
bestimmt werden.
For. 6: Gleichungssystem zur Ermittlung der Fehlergrößen
Für die Korrektur eines Fehlers wird das Komplement der Fehlergröße zu dem Symbol an der Fehlerposition hinzuaddiert. Anschließend ist die ursprüngliche Nachricht wiederhergestellt.
Jetzt da alle Grundlagen bekannt sind, soll ein Beispiel den Encodingprozess verdeutlichen. Dabei werden nacheinander die folgenden sechs Schritte durchlaufen.
In diesem Beispiel werden die Daten "01234567" in einen QR Code mit dem Fehlerkorrektur Niveau M (Referenz 00 -- siehe Tabelle 3) abgelegt. Dafür analysieren wir zunächst die Daten. Es handelt sich nur um Ziffern, deswegen ist der Numeric Mode (Mode Indicator = 0001 -- siehe [Informationen in QR Code Symbolen: Tabelle 2]) optimal. Der Character Count Indicator beträgt 8, da die Daten aus 8 Ziffern bestehen (CCI = 8 bzw. 000000100).
Anschließend suchen wir die optimale Version für das Symbol. Dabei wird immer die kleinste Version herausgesucht, die mehr oder genauso viele Daten enthalten kann, wie durch das Fehlerkorrektur Niveau und den Modus vorgegeben sind. In diesem Fall kann schon Version 1-M 34 (>= 8) Ziffern enthalten (siehe [Informationen in QR Code Symbolen: Tabelle 1]).
Als nächstes müssen wir die Versionsinformationen berechnen, aber unser Symbol der Größe 1-M benötigt diese nicht (Versionen < 7).
Dann encodieren wir die Daten analog zum Beispiel im Kapitel Numeric Mode.
Der Terminator kann in Informationen in QR Code Symbolen: Tabelle 2 nachgelesen werden und hat die Referenz 0000.
Wir konkatenieren die Daten und ergänzen 3 Füllbits (0en), um auf die Größe des nächsthöheren Codeworts zu kommen.
Anschließend müssen die 10 (16 CW - 6 CW) verbleibenden Codewörter der Version 1-M aufgefüllt werden. Dafür können wir eine beliebige Bitfolge verwenden.
Für die Datencodewörter werden noch die Fehlerkorrekturdaten berechnet und konkateniert.
So ergeben sich alle Codewörter, die im Symbol gespeichert werden müssen.
Jetzt füllen wir eine Anfangsmatrix mit diesen Daten und wenden alle Masking Patterns darauf an. Wie im Masking Kapitel beschrieben, wählen wir die beste Masking Pattern Referenz, in diesem Fall 011, aus.
Mit diesen Informationen können wir dann die Formatinformationen wie in dem Beispiel des entsprechenden Kapitels errechnen und einfügen. Das ganze ist schematisch in Abbildung 2 dargestellt.
Abb.2: Die Ausgangsmatrix wird mit allen Masken kombiniert
Daraus resultiert der endgültige Code (siehe Abbildung 3).
Abb.3: Endgültiger Code
Um ein QR Code Symbol zu decodieren muss dieses als Bild vorliegen. Dann gibt es eine kurze Erkennungsphase in der das Symbol gefunden, normalisiert und digitalisiert wird. Anschließend wird das Bild nicht mehr benötigt, da die weitere Analyse auf den Daten aufbaut.
Der Decodingprozess ist viel komplizierter als das Encodingprozess und wird im Standard nur als Pseudocode beschrieben. Die konkrete Implementation der einzelnen Funktionen bleibt offen. In Abbildung 3 ist der Ablauf in Form eines Flussdiagrammes abgebildet.
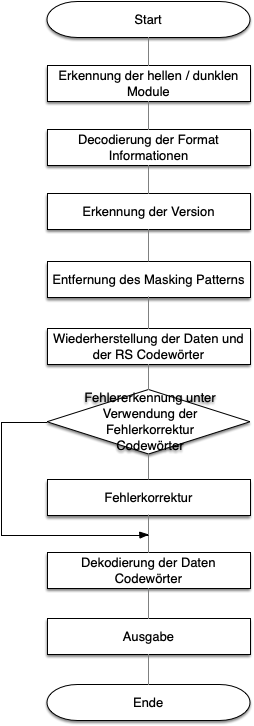
Abb. 3: Flussdiagramm des Decoding-Prozesses
Es folgt eine ausführlichere Beschreibung des Decodings.
,
und die
Distanz D zwischen ihnen abgelesen (siehe Abbildung 4), sodass
die Modulgröße 
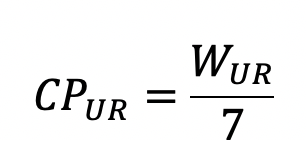und die vorläufige Version
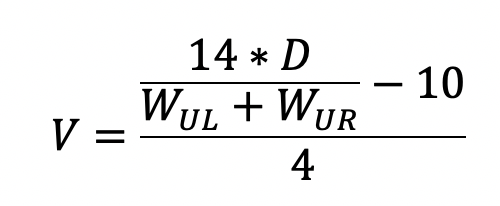berechnet werden kann.
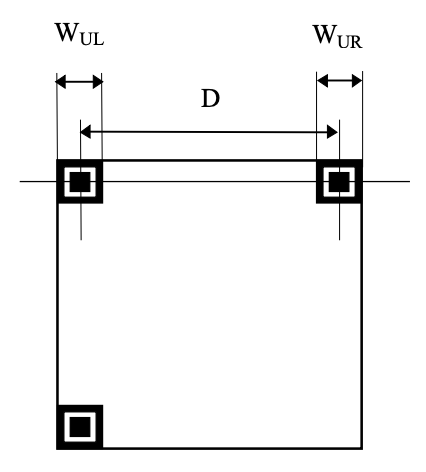
Abb. 4: Breite der Finder Patterns und Distanz zwischen ihnen